Курс посвящен введению в математическую теорию построения генераторов псевдослучайных последовательностей (ПСГ) применительно к синтезу поточных шифраторов и вопросов защиты информации в вычислительных системах и сетях. ПСГ - суть автономный автомат, который, на самом деле, является автономной 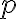 -адической динамической системой.
-адической динамической системой.
В самом общем виде, динамика – раздел математики, изучающий действия полугруппы 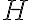 на фазовом пространстве
на фазовом пространстве 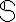 , которое является измеримым, т.е.
, которое является измеримым, т.е. 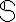 наделено мерой
наделено мерой 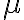 , и
, и 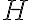 действует на
действует на 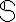 преобразованиями
преобразованиями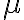 . Часто предполагается, что
. Часто предполагается, что 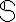 наделено также метрикой
наделено также метрикой 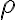 , и
, и 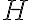 действует преобразованиями
действует преобразованиями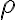 . Говоря об алгебраической динамике, дополнительно предполагают, что пространство наделено не только метрикой и мерой, но и обладает алгебраической структурой (т.е.
. Говоря об алгебраической динамике, дополнительно предполагают, что пространство наделено не только метрикой и мерой, но и обладает алгебраической структурой (т.е. 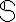 является универсальной алгеброй).
является универсальной алгеброй).
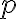 -Адические динамические системы представляют собой один из разделов алгебраической динамики – динамики на алгебраических системах (полях, кольцах, группах) со структурой проективного предела. Структура проективного предела, в свою очередь, порождает ультраметрическу
-Адические динамические системы представляют собой один из разделов алгебраической динамики – динамики на алгебраических системах (полях, кольцах, группах) со структурой проективного предела. Структура проективного предела, в свою очередь, порождает ультраметрическу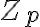 целых
целых 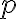 -адических чисел, которое, на самом деле, является проконечной алгеброй со структурой проективного предела: кольцо
-адических чисел, которое, на самом деле, является проконечной алгеброй со структурой проективного предела: кольцо 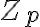 может быть представлено как проективная система колец вычетов
может быть представлено как проективная система колец вычетов 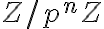 ,
, 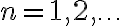 ; а, автоматные отображения, в свою очередь, как непрерывные преобразования пространства
; а, автоматные отображения, в свою очередь, как непрерывные преобразования пространства 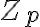 относительно
относительно 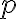 -адической метрики. Важнейшими характеристиками динамики являются ее эргодичность и сохранение меры. Для синтеза ПСГ как раз и используются именно эргодические и сохраняющие меру отображения.
-адической метрики. Важнейшими характеристиками динамики являются ее эргодичность и сохранение меры. Для синтеза ПСГ как раз и используются именно эргодические и сохраняющие меру отображения.
- Teacher: Ливат Борисович Тяпаев